
The reason we've selected this is because it's very common in physics, in particular it is used in relativity theory, general relativity and even in relativistic quantum field theory. The first example we present to you is a bit obscure, but we hope you can excuse us, as we're physicists, for starting with this very important type of space: Minkowski space. Also, you will hopefully understand why we are not going to bother calculating distances in other spaces. However, we can try to give you some examples of other spaces that are commonly used and that might help you understand why Euclidean space is not the only space. We do not want to bore you with mathematical definitions of what is a space and what makes the Euclidean space unique, since that would be too complicated to explain in a simple distance calculator. Euclidean space can have as many dimensions as you want, as long as there is a finite number of them, and they still obey Euclidean rules. Let's also not confuse Euclidean space with multidimensional spaces. This is something we all take for granted, but this is not true in all spaces. In Euclidean space, the sum of the angles of a triangle equals 180º and squares have all their angles equal to 90º always. The Euclidean space or Euclidean geometry is what we all usually think of 2D space is before we receive any deep mathematical training in any of these aspects. Since this is a very special case, from now on we will talk only about distance in two dimensions. If you wish to find the distance between two points in 1D space you can still use this calculator by simply setting one of the coordinates to be the same for both points. For each point in 2D space, we need two coordinates that are unique to that point. These points are described by their coordinates in space.
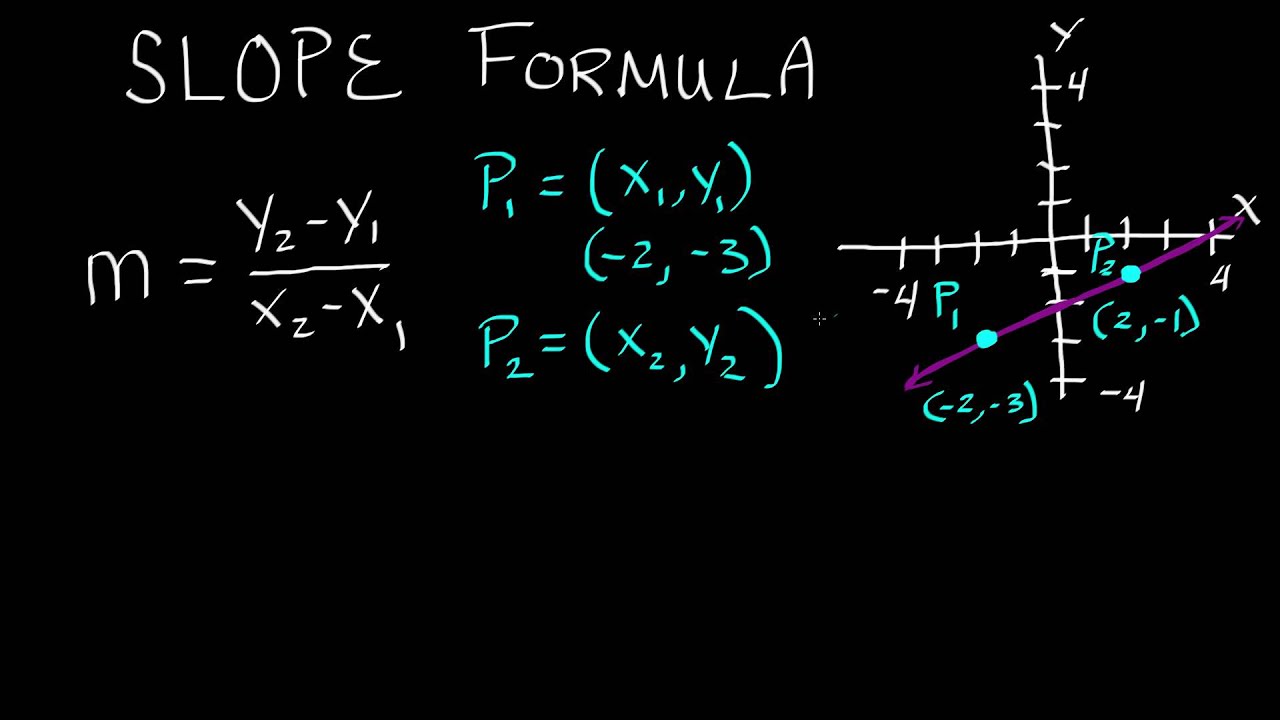
To find the distance between two points, the first thing you need is two points, obviously. If you are looking for the 3D distance between 2 points we encourage you to use our 3D distance calculator made specifically for that purpose. For this calculator, we focus only on the 2D distance (with the 1D included as a special case). In most cases, you're probably talking about three dimensions or less, since that's all we can imagine without our brains exploding. If we stick with the geometrical definition of distance we still have to define what kind of space we are working in. You will see in the following sections how the concept of distance can be extended beyond length, in more than one sense that is the breakthrough behind Einstein's theory of relativity. This definition is one way to say what almost all of us think of distance intuitively, but it is not the only way we could talk about distance. The most common meaning is the 1D space between two points.
#Slope and distance formula geometry how to
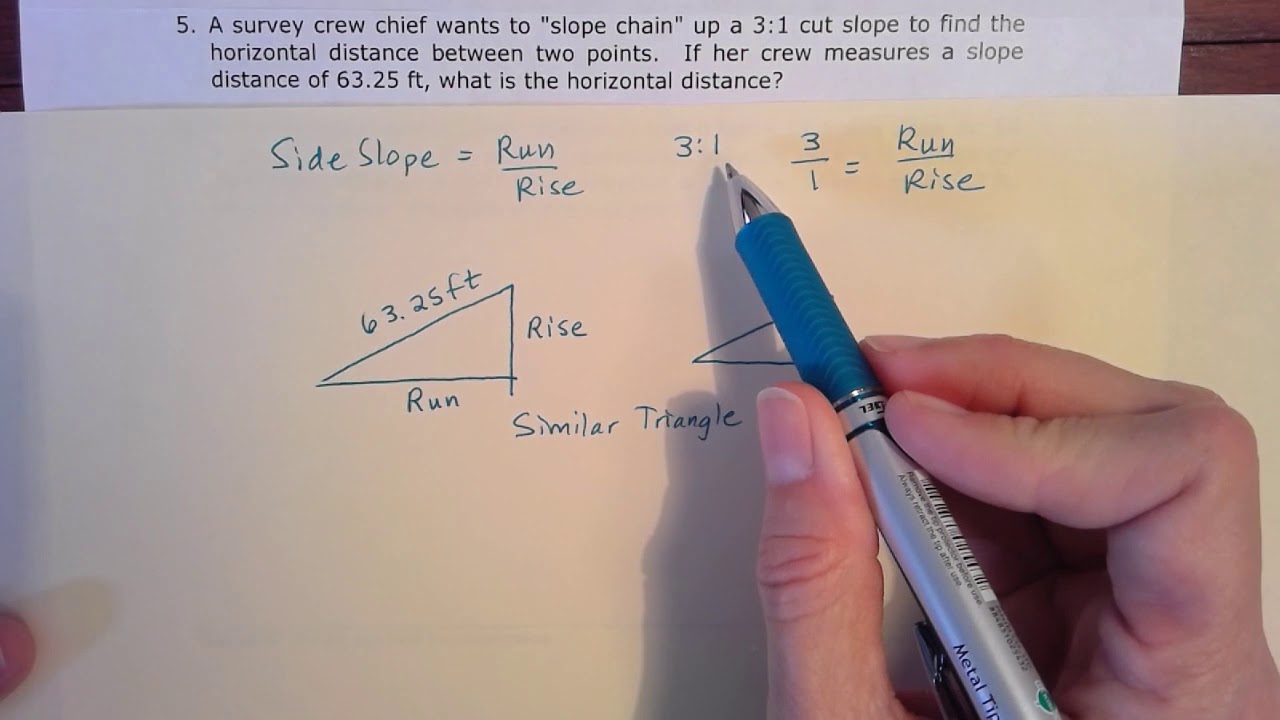
The legs of this triangle would be parallel to the axes which mean that we can measure the length of the legs easily.Before we get into how to calculate distances, we should probably clarify what a distance is. We could see the line drawn between these two points is the hypotenuse of a right triangle. We want to calculate the distance between the two points (-2, 1) and (4, 3). We'll explain this using an example below The distance formula is used to find the distance between two points in the coordinate plane.


 0 kommentar(er)
0 kommentar(er)
